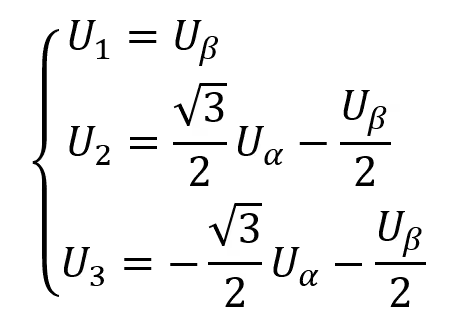https://www.bilibili.com/read/cv17009556/

前陣子在網路上看到一個視頻，講的真不錯，視頻資源鏈接放在下面，對電機控制有興趣的可以去看看：

TI嵌入式研討會集錦-賦予舊的馬達新的技巧

不過對於這套東西要說起來也不是很難理解，下面我將深入淺出的介紹下這套算法以及實現方式，當然如果有哪裡理解或者解釋不到位或者由偏差的，歡迎在下方評論區討論告知。

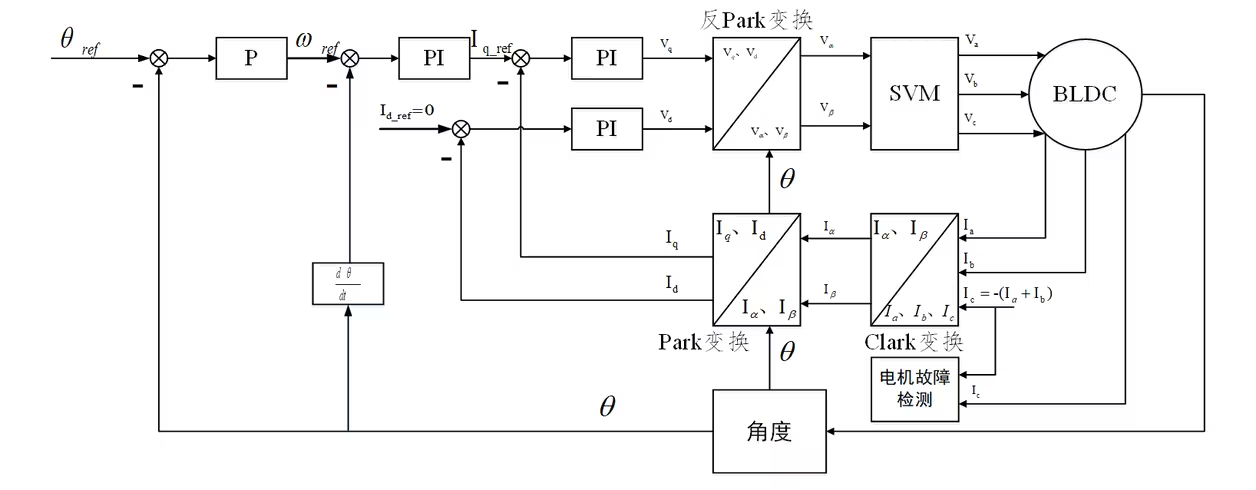
場定向控制演算法也就是所謂的FOC(Field Oriented Control)，這裡的場指的是磁場和電場，也被翻譯為向量控制。此控制演算法可用於永磁同步馬達(PMSM)和三相無刷直流馬達(BLDC)，常用在高效能的馬達運用場景。該演算法由Siemens的一位研究人員Felix Blaschke構想出來的，本質上是一種扭矩控制演算法，控制結構框圖如下所示。

圖1 FOC演算法控制結構框圖

這個框圖就是FOC的精髓了哈，把這個都搞懂就啥都明白了！對於學過自控原理的同學來說，這種結構框圖應該會很熟悉哈，從FOC演算法的控制結構框圖看出，無刷直流馬達的控制輸入量是設定轉速，透過一個比例積分器計算出交軸電流量，再透過一個比例積分器計算出的量為交軸電壓量Vq，下面的Vd為直軸電壓量，交軸和直軸是在同步馬達中提出的概念，交軸的英文為quadratur，直軸的英文為direct，在永磁同步馬達或直流無刷馬達中，勵磁繞組所纏繞的極靴與永磁體之間電磁力可以分解為垂直於轉子的力和一個沿轉子切線方向的力，垂直於轉子的力的方向稱為直軸，沿轉子切線方向稱為交軸。

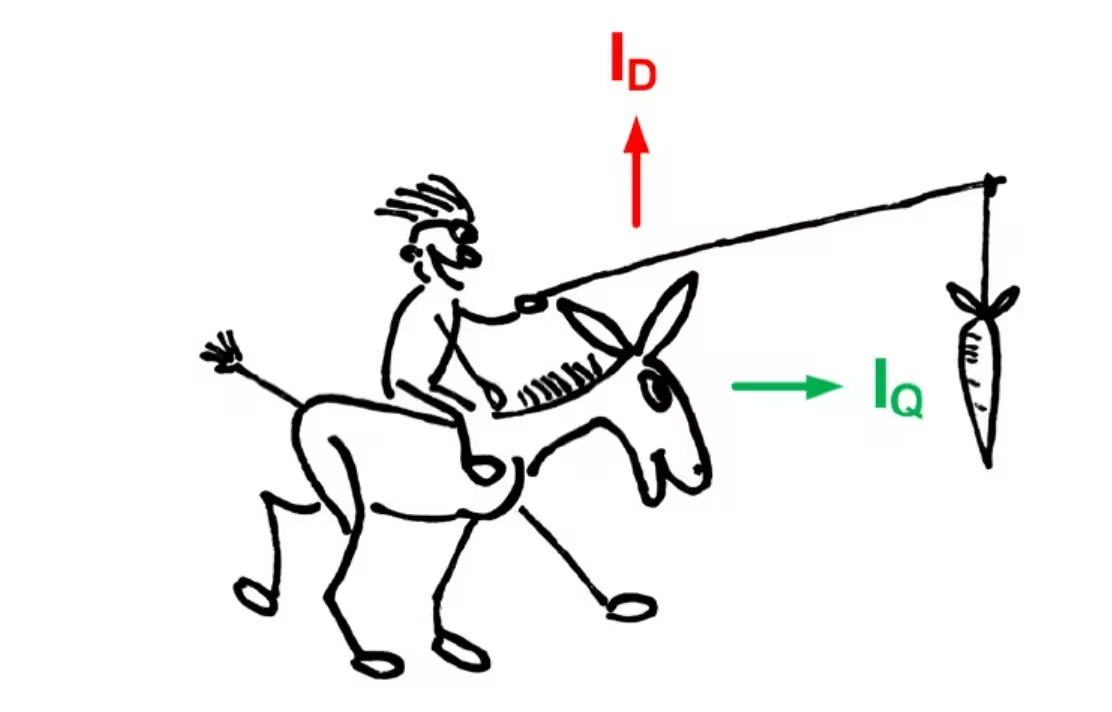
關於直軸和交軸，它們是什麼意義呢？我在網路上找到一張圖，感覺很形像生動，就像這樣：

圖2 直軸交軸形象化理解示意圖

可以這麼理解這張圖，我們知道馬達的工作原理是電磁效應，將電磁效應用到了極致，線圈與外邊的永磁體（我們這裡所說的永磁同步馬達和無刷直流馬達都是屬於永磁系列）之間有電磁力的作用，力是一個向量，可以分解為垂直於轉子切線的直軸電磁力和沿切線方向的交軸電磁力。

透過反Park變換得到旋轉座標系下的電壓控制量vα和vβ，再透過SVPWM演算法將控制量調變到三相逆變電路上，進而控制馬達旋轉。 Park變換是分析同步馬達的常用座標變換演算法，後文會對此變換進行詳細介紹。

反饋量是馬達的單相電流值，此處只收集了兩相電流值是因為根據基爾霍夫電流定律可計算出第三相的電流值。三個電流取樣值經由Clark變換得到兩相旋轉座標系下的電流值Iα和Iβ，再透過Park變換得到兩相靜止座標系下的電流值Ia和Ib，此變換的具體內容將在後文詳細敘述。

另外一個反饋量是馬達的位置訊號，位置訊號可採用有感測器模式，例如添加磁編碼器或光電編碼器得到馬達的位置訊號，另外也可以採用無感測器模式，直接透過測量馬達三相電流值，設計狀態觀測器計算馬達位置值。

透過SVPWM將矯正電壓調製到馬達端子上。

在前面一小節中詳細介紹了FOC控制演算法的控制想法和流程，其中涉及兩種矩陣變換，分別是Park變換和Clark變換。需要注意到一個事實，透過逆變電路得到的電流已經不是直流電了，也就是說這裡的Ia、Ib、Ic是交流信號了，從控制上來講，交流信號是很難作為反饋量進行反饋的，工程師希望將交流訊號轉換為直流訊號，這就是Park變換和Clark變換的意義。

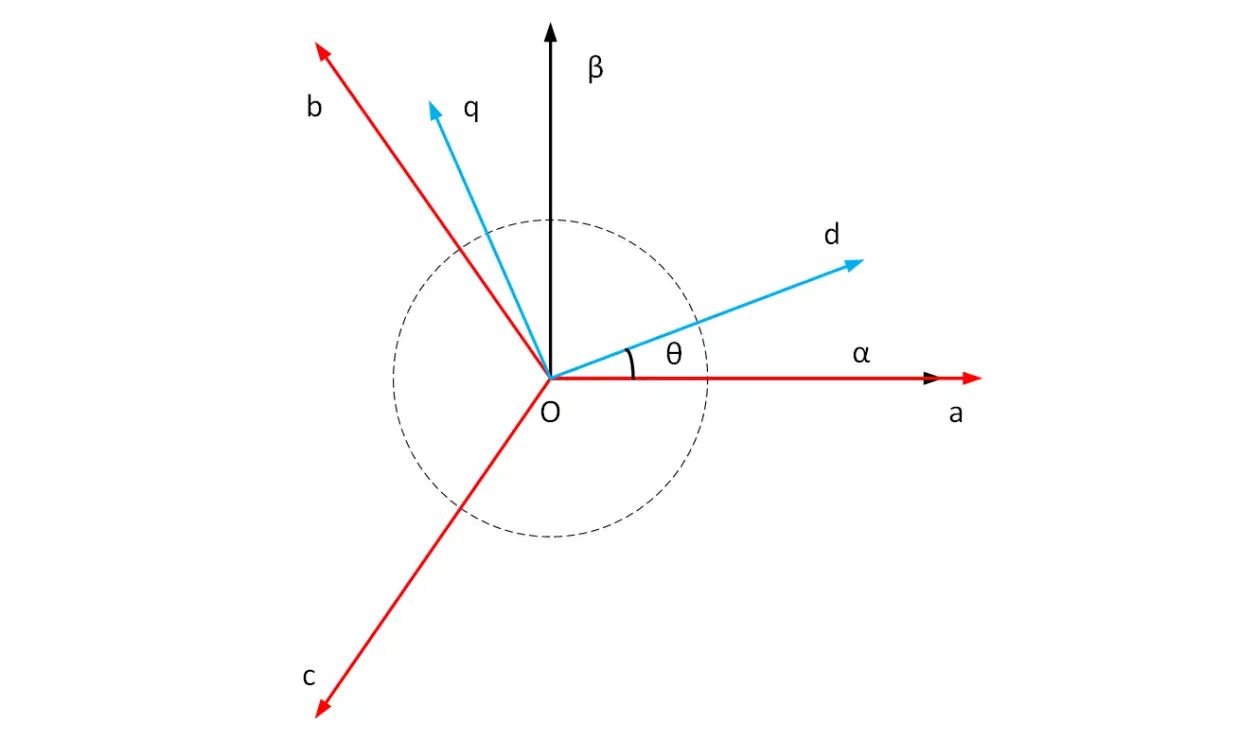
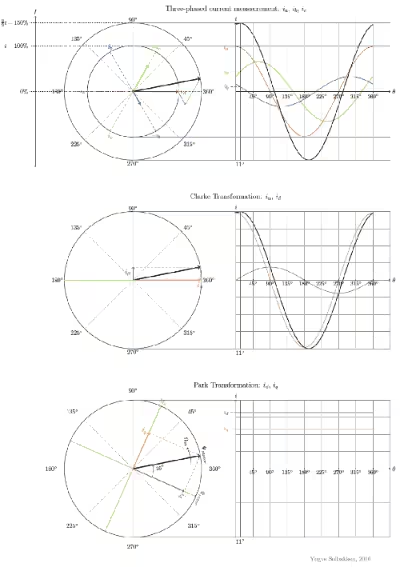
三相無刷直流馬達的勵磁繞組部分一般是星形接法，夾角為120°，這裡的120°表示的是電角度，在二維平面上可以用圖3.13所示。在a、b、c三個軸上的電流是時刻變化的，假設是正弦信號，它們之間的相位差為120°(在這種假設情況下，電機是勻速轉動的，轉速與頻率有關) ，以a軸為x軸，建立一個直角座標系，只不過座標軸分別記為α軸和β軸。這裡的做法是將a、b、c三個軸上的空間電流向量訊號透過向量分解，分解到直角座標系下。如果能夠即時取得到轉子旋轉的角度值θ ，就可以將直角座標系旋轉pθ 度(p為極對數)，即將αOβ這個直角座標系整體旋轉θ度建立另外一個座標系dOq，剛好就可以巧妙的消去原始的正弦量，得到兩個直流訊號Id和Iq，將這兩個直流訊號做為回授量。這其實就是Park變換與Clark變換的基本想法。

圖3 Park變換與Clark變換

Clark變換與Park變換其實是在做電流的解耦操作，方便反饋使用，之所以在三相無刷直流電機力矩分析過程中一般使用電流這個物理量，是因為電流決定了電磁力矩變化，在無刷直流馬達中，力矩與電流的關係為：

P為三相無刷直流馬達的極對數，若馬達的勵磁繞組是可見的，直接數極靴的數，除以3就是極對數。如果勵磁繞組是看不見的，將馬達兩相通電，電機會呈現一種多檔開關的效果。然後扭動馬達轉子旋轉一周，感受到有幾次停頓就表示有幾對極。極對數是非常重要的一個量，在後文中的確定電機參數會再次提到。 λdr為馬達的電磁轉矩係數，Iqs為馬達的每相勵磁繞組的電流值。

具體來看，Clark變換做的操作就是將三個相隔120°的正弦信號分解成一個相隔90°的正弦信號，需要注意的雖然少了一個正弦信號，但是他們的疊加值是相等的。但這是不夠的，裡面還是有一個不確定的值θ ，這是馬達轉子的電角度。我們再想，如果我們能知道這個角度值θ ，能不能讓座標繫跟著轉子一起轉呢？ ，這樣是不是就把這個θ 抵消掉了。一研究發現，呦，這個電角度不是和機械角度有個極對數P的關係嗎，機械角度是可以透過編碼器測量到的，如果我能夠實時獲得這個角度值，不就沒有未知量了嘛~！這就是Park變換在做的事情~，回來去看看那個FOC框圖的下面回饋的部分，是不是就清晰很多。至於這個θ 怎麼獲取就看本事了，加感測器就是所謂的有感，不加感測器就需要透過一些其他手段獲取，這就是所謂的無感，這下都明白了吧！

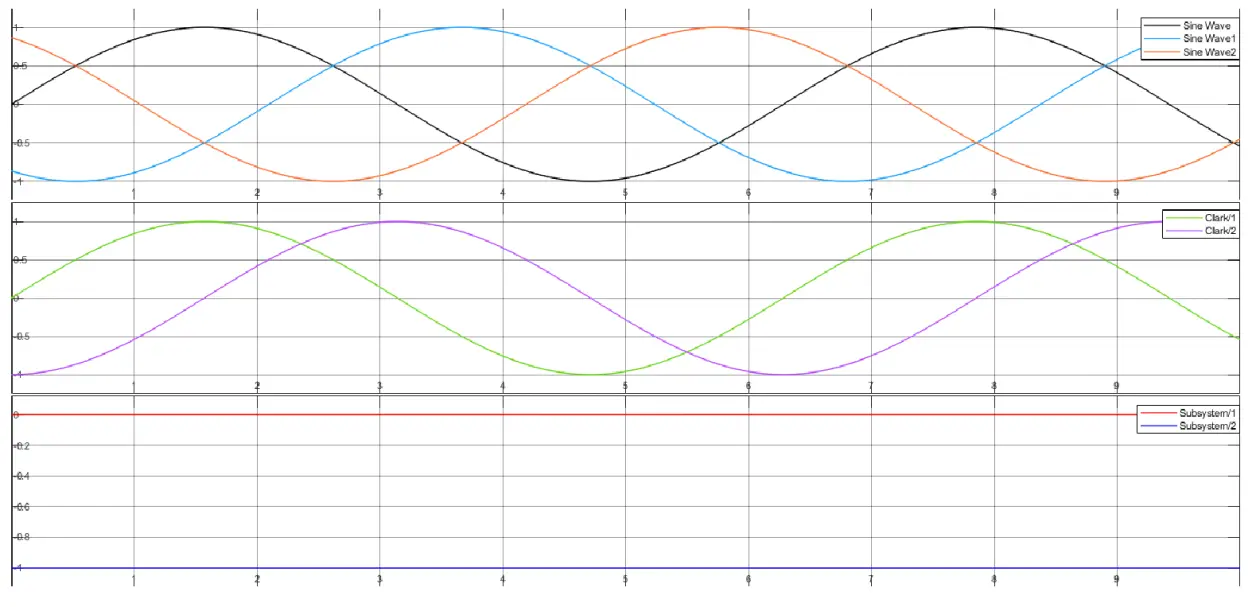
我在Simulink中搭建了一個簡單的模擬模型來模擬這個過程，結果就像這樣：

圖4 Park與Clark變換模擬圖

如果這個靜態的圖看起來不夠生動，下面這個動態圖比較像：

圖5 Park與Clark變換動態圖

仔細看看是不是就是這個過程，是不是很直覺！透過Clark變換和Park變換將三個相隔120°的正弦訊號轉變為兩個直流訊號，但是目標不變。

前面一段的結尾引用部分我解釋的第一個問題中就提到了一種神奇的演算法，這種神奇的演算法就是這段要叫的SVPWM演算法啦，這個演算法要說明白可真不容易，不然為啥叫神奇的演算法呢！ SVPWM和我們在大學階段接觸到的PWM和SPWM功能上是一樣的，目的就是把控制量轉換一種形式加到馬達的三個端子上，這個動作電控領域的大佬們給取了個名字叫做調製，英文叫做Modulation。

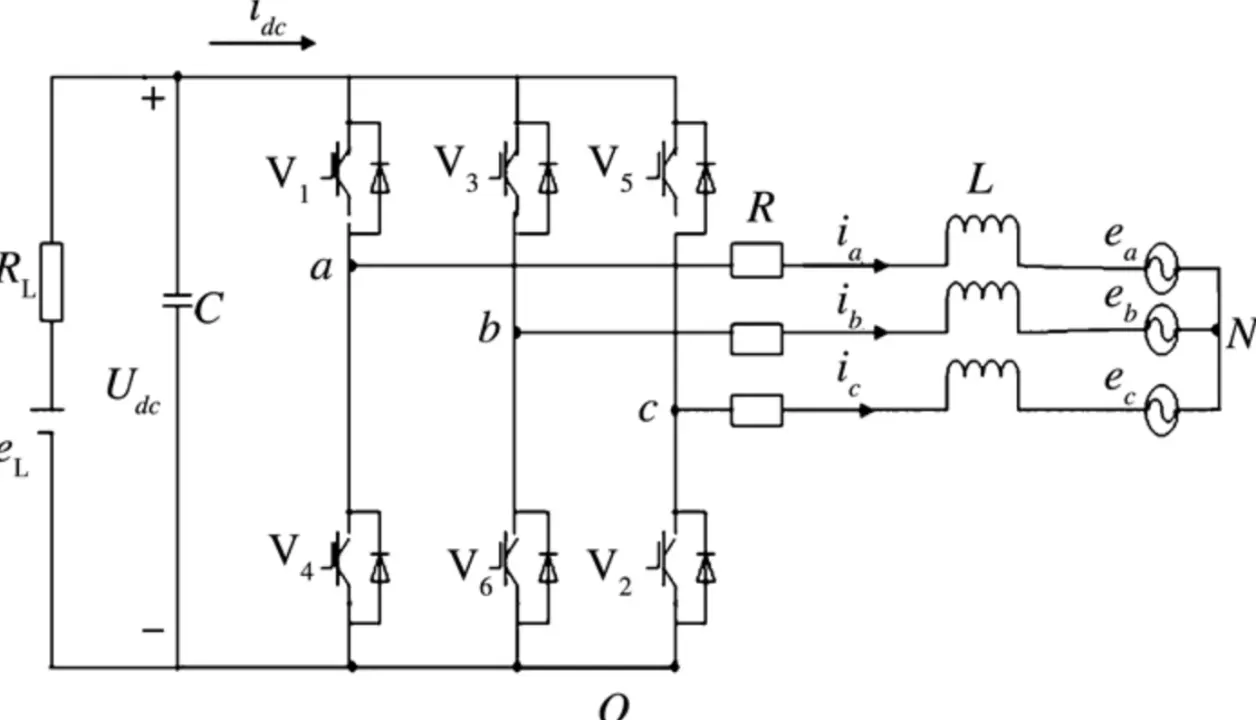
無刷馬達的驅動電路一般是三相逆變電路，由三個半橋組成的，就長這樣：

圖6 三相逆變電路

上圖是三相無刷直流馬達的驅動原理圖，馬達內部的勵磁繞組是星型(記作Y型)連接，驅動由6個MOS管組成三相逆變電路。 MOS管低電壓端由MCU控制，上面三個MOS管S1、S3、S5構成逆變電路的上橋臂，下方三個MOS管S2、S4、S6稱為下橋臂。同一相上下橋臂不能同時導通，同時導通同一相上下橋臂會造成電源短路。因此實際上控制端只需要三根控制線即可，MOS管依序用S1，S2，S3，S4，S5，S6來表示，如圖所示，上橋臂MOS管導通為1，關斷為0 ，共有八種組合方式，分別是000，100，010，001，110，101，011，111。

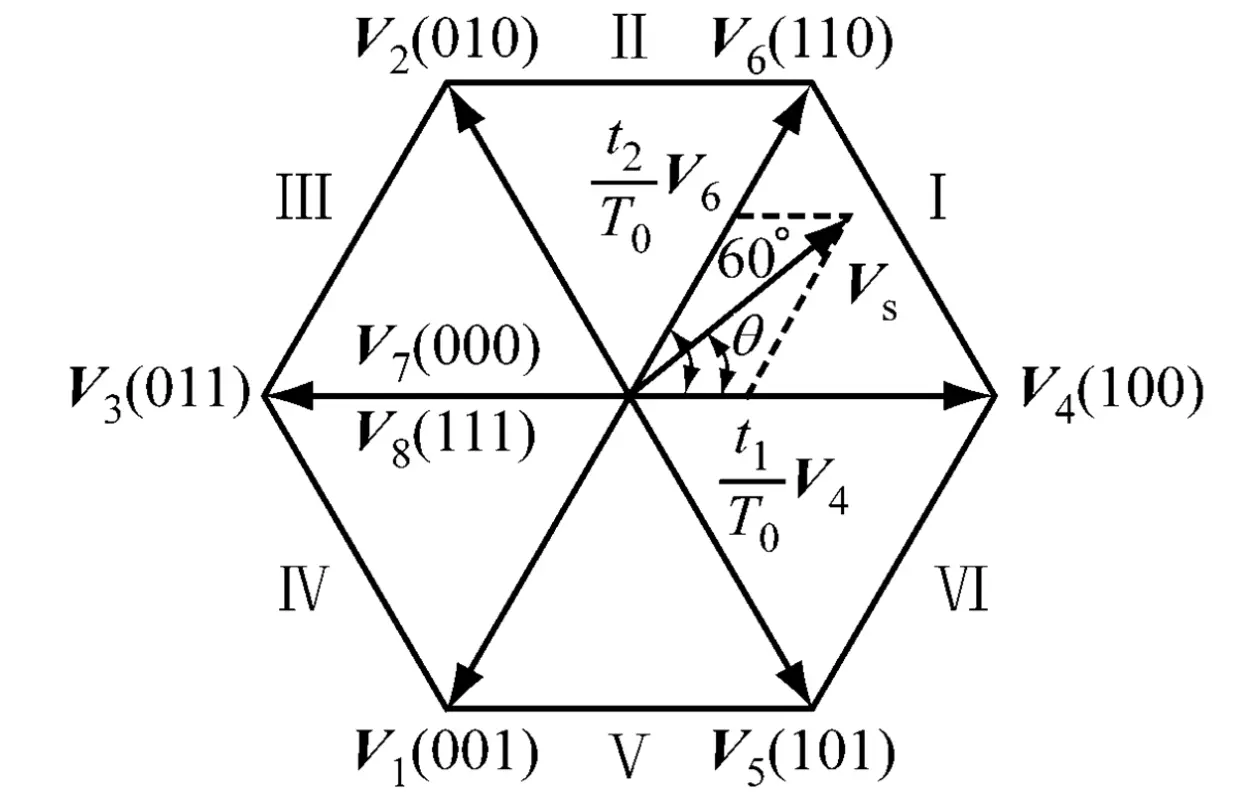
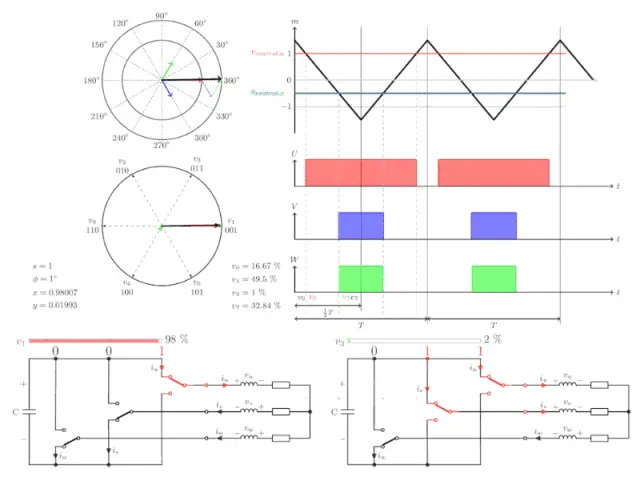
無刷直流馬達的驅動方式由最開始的六步方波逐步改進為六步正弦波，再到後來的FOC以及直接轉矩控制。六步方波是上面提到的八步去除了000和111的狀態，剩下的六步根據轉子位置依次施加到逆變電路上的狀態。六步驟正弦波是在六部方波的基礎上所做的改進，這兩種演算法曾經使用是非常廣泛的，由於本文的篇幅限制，這裡不與討論。本文採用的是FOC演算法，因此對FOC做詳細描述。透過逆變電路將電流輸入到馬達的三個引線端子上。無刷直流馬達內部的勵磁繞組一般依照星形接法，在三相無刷直流馬達控制過程中，電流是從其中兩相輸入，另外一相作為輸出，這裡涉及電壓空間向量的概念，和電流空間向量類似。透過控制其中兩相電壓的大小，來控制電壓空間向量的大小和方向，圖中Vs就是電壓空間向量，是由三相中的兩相電壓合成的。每一相電壓的大小並不能控制，而是透過控制每一相導通的時間，計算單位時間內各相的平均電壓作為這一相的電壓值，所以可以說SVPWM的理論基礎是平均值等效原理。於是為了方便分析，電控領域的天才大佬們想出一種圖來描述這個過程，如下圖：

圖7 空間電壓向量圖

依照逆變電路中的導通情況分了八種狀態，將這八種狀態與電壓空間對應起來則可以得到空間向量圖，總共劃分了六個扇區，分別用Ⅰ、Ⅱ、Ⅲ、Ⅳ、 Ⅴ、Ⅵ表示，每個扇區為60°。

這張圖很重要，弄清楚這張圖，就弄清楚了SVPWM。這是不是跟前面一樣，可以感受到身為工程師，他們都很喜歡這樣的圖的。圖裡面的Vs就是目標向量，我們要透過圖中的把八個向量合成這個Vs（V7和V8是零向量，就是大小為零，方向隨意），要怎麼合成呢？很簡單啊，舉個例子，如果你這個目標向量想要在第一象限，我導通V4和V6不就行了，嗯！思路是對的，那麼下面問題就來了，我想控制合向量在第Ⅰ象限一個具體的位置。問題是（1）你怎麼告訴我，我怎麼知道你是要在第一象限，我們回過頭來看看前面那個結構框圖，SVPWM的輸入是什麼？是不是Vα和Vβ啊，就是說對於SVPWM而言，它只知道Vα和Vβ ，其他的它不知道，它要做的工作之一就是透過這個Vα和Vβ 得到控制器想要控制空間向量的目標象限。 （2）如果解決了第一個問題，那麼SVPWM就知道了目標了空間向量了，那自然就知道導通哪兩個狀態，現在是怎麼控制這兩個狀態的向量大小？大小是透過控制導通的時間來控制的，這個時間怎麼算，這是SVPWM要解決的第二個問題。

具體過程這裡不介紹了，直接給結論：

圖8 SVPWM扇區判斷表一

其實有表一已經足夠工程師們快速判斷目標空間電壓向量所在的磁區，但是在單晶片中設計程式實現磁區判斷的時候，希望能夠有更簡單的演算法。進一步研究發現，目標空間電壓向量由下式決定：

圖9 空間電壓向量計算簡化公式

設三個變數A，B，C，當U1>0時，A=1，否則A=0；當U2>0時，B=1，否則B=0；當U3>0時，C=1，否則C=0。令X=A+2B+4C，透過X的值可以快速判斷目標電壓空間向量Uref所在磁區，把這個對應關係列表如下所示：

圖10 空間電壓向量導通時間計算表二

具體過程就不細說了哈，有興趣的可以找一些資料看。這連個問題一解決，SVPWM的主要工作就結束了哈，這樣調製到馬達三相上的電壓就是正弦量了，很神奇吧！這兩個表是在後面驅動程式設計會用到，非常重要。下面看一個動態圖，完全概括了這個過程，非常形象化。

圖11 BLDC控制動態圖

讀到這裡，我們才初步感受到TI工程師為啥說為了讓這個馬達一圈一圈轉起來還真費老鼻子勁了。

理論部分結束了，就要開始實踐部分了，畢竟這些東西要是純粹留在紙上是沒有任何價值的，我們需要把它用到實際中來。我開發了一個FOC驅動器，外觀長這樣。

圖12 FOC驅動器

韌體部分尚未調通，調通之後整個專案會開源，本文未完待續~~~。 作者：友善的橘子

43 person(s) visited this page until now.

Back