https://zhuanlan.zhihu.com/p/683882301

本文先闡述FOC控制演算法的最後一步－SVPWM，即空間向量脈寬調變。本文將結合理論從程式碼角度去分析SVPWM演算法，逐步解析其如何將輸入的目標電壓值Uout轉換為PWM佔空比的。 FOC控制庫中SVPWM的實作函數是PWMC_SetPhaseVoltage，在原始碼檔案pwm_curr_fdbk.c。

網路上有很多關於SVPWM演算法原理的講解，但很少有結合實際程式碼實作去講解的，大多數文章跟實際並不相關。本文結合程式碼，加上一些個人理解，為大家梳理SVPWM，讓大家對演算法有更深入的理解。

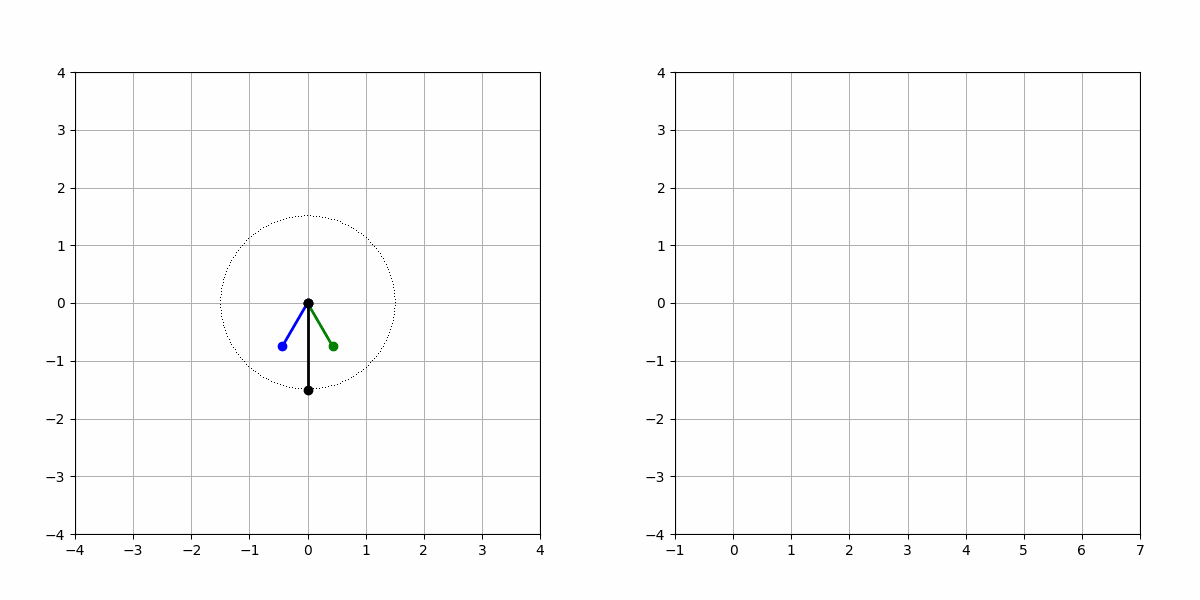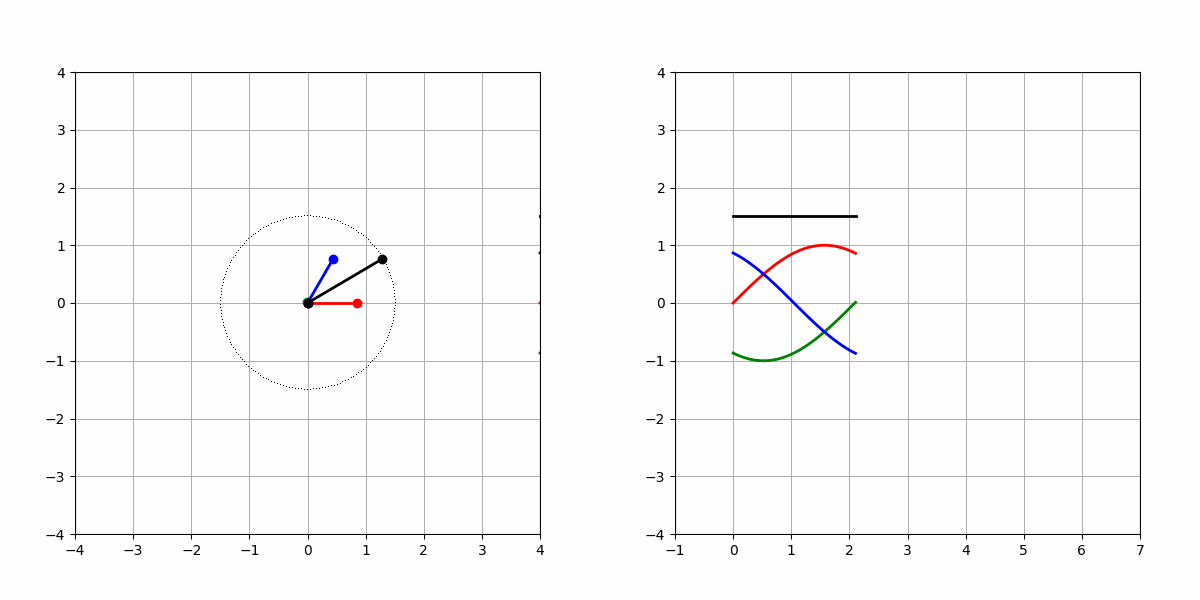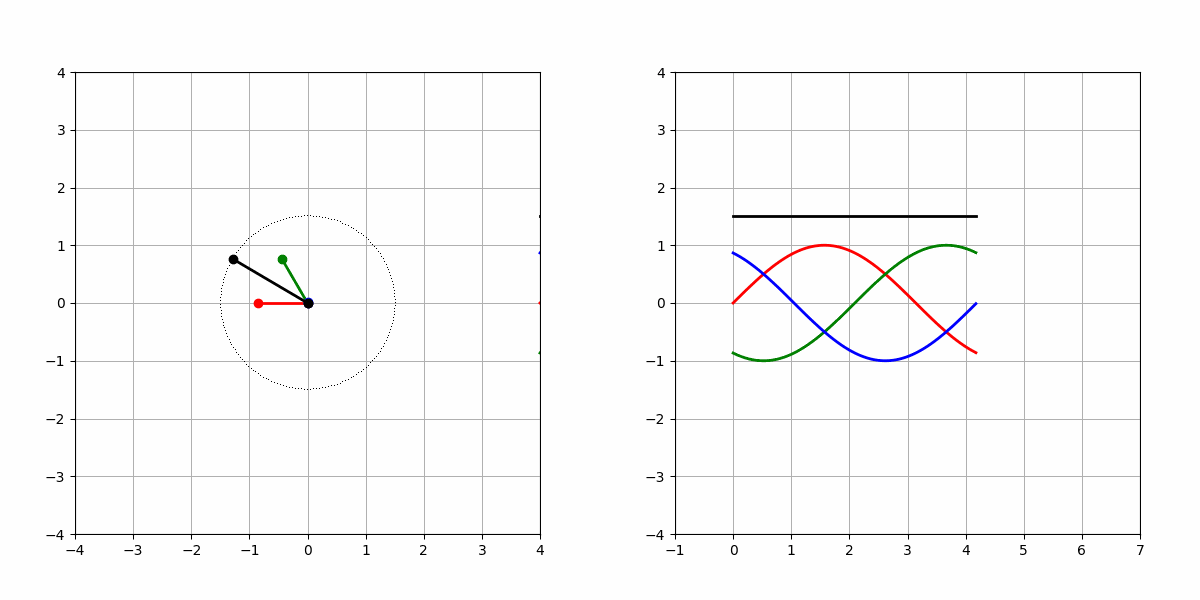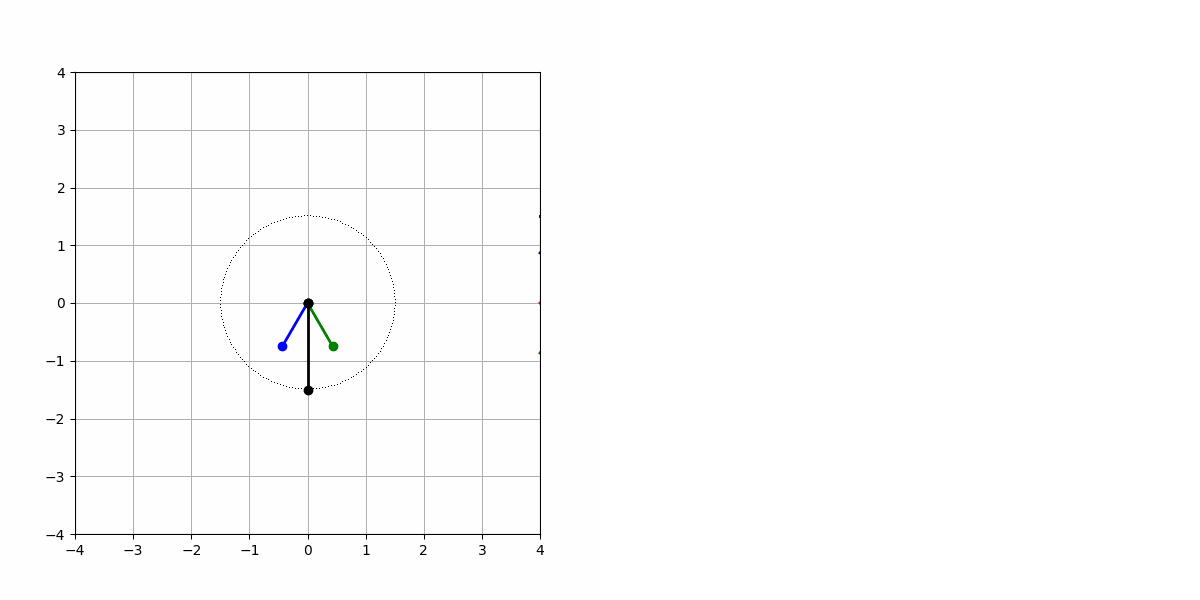
如圖1所示，UVW三相電壓顏色為別為紅色、綠色和藍色，合成的電壓向量為黑色，左圖為電壓向量合成示意圖，右圖為電壓的模長隨時間ωt變化示意圖

動圖封面 圖1 電壓向量合成動圖

電機中UVW三相在空間位置上相差120度(這是電角度，其等於機械角度乘以極對數)，電機運轉過程中三相電壓分別為Uu、Uv和Uw。現在以U相為基準建立αOβ平面直角座標系，則可以寫出三相電流的表達式：

由上面表達式可以得到兩個結論：

三相電壓的標量和等於零：Uu+Uv+Uw=0，證明過程如下：

三相電壓的向量和為半徑為3/2的圓：r=3/2，證明過程如下：

圖2 電壓向量正交分解

如圖2所示，將Uu、Uv和Uw依照直角座標系分解，可以得到：

同理可證得：

由此可得：

這個結論說明了相電壓是母線電壓的2/3，後面會用到

函數輸入是Valfa_beta，涵義是圖2中α和β軸的分量大小

uint16_t PWMC_SetPhaseVoltage( PWMC_Handle_t * pHandle, alphabeta_t Valfa_beta )

pHandle→hT_Sqrt3的宏定義為2*sqrt(3)，暫時忽略掉入參wUAlpha和wUBeta中的PWM週期Ts和電壓分量，只把它當作角度來分析，則wUAlpha為：2*sqrt(3)*α，wUBeta為：-2*β

int32_t wUAlpha = Valfa_beta.alpha * ( int32_t )pHandle->hT_Sqrt3;
int32_t wUBeta = -( Valfa_beta.beta * ( int32_t )( pHandle->PWMperiod ) ) * 2; 
#define SQRT3FACTOR (uint16_t) 0xDDB4 /* = (16384 * 1.732051 * 2)*/

程式碼中給了三個分量wX，wY和wZ

int32_t  wX = wUBeta; 
int32_t  wY = ( wUBeta + wUAlpha ) / 2; 
int32_t  wZ = ( wUBeta - wUAlpha ) / 2;

由此得到:

由此可以得到三條直線方程式：

如圖3所示，三條直線將直角座標系分為六個磁區

圖3 扇區劃分

圖4 線性區域規劃

如圖4所示，根據中學學過的線性區域規劃的知識，可以得到：紅色部分為wX>0的區域，綠色區域為wY>0的區域，藍色區域為wZ>0的區域，由此可以得到表1的結果。程式碼中先依照wX，wY和wZ的值進行磁區判斷，計算PWM佔空比

表1 扇區判斷表

例如wY < 0，wZ < 0即可判斷目標向量落在磁5(SECTOR_5)區內

if ( wY < 0 )
 {
 if ( wZ < 0 )
 {
  pHandle->Sector = SECTOR_5;
 }
}

我們來分析第6扇區的空間向量合成情況，SVPWM波形是7段式，根據程式碼可以看出三相佔空比大小是A>B>C，即第六扇區7段式為：0- 4-5-7-5-4-0。波形如圖6所示

圖5 三相電壓通電時間

圖6 六個基本空間向量

FOC庫中配置的定時器工作模式是中心對齊模式(定時器CNT計數值增加到等於定時週期時，再遞減到0，如此往復循環)，如此可以得到如圖5的波形。從圖中得出結論，T4=Tx，T5=Ty，T7=T0=(Ts-Tx-Ty)/2。狀態7和狀態0合成的向量為零向量，不對電機做功如圖6，這裡我們分析第六扇區的情況，U4為100，代表U相；U5為101，代表U相和W相的合成向量，Tx是U4的通電時間，Ty是U5的通電時間。同樣這裡我們把Uout正交分解，則有：

根據「空間向量合成」中的結論二，可以將U4和U5替換為2*Udc/3，將其帶入上式，可以得到：

Uout在α軸上的分量為U_out*cos⁡(Θ)，在β軸上的分量是U_out*sin⁡(Θ)，這裡寫成Uα和Uβ。Udc/sqrt(3)為合成的最大不失真電壓，原因放到下一節講，這裡的Uα/(Udc/sqrt(3))為alpha，Uβ/(Udc/sqrt(3))為beta，alpha和beta這兩個值為SVPWM函數的入參

在「六個扇區劃分」開始時，我們知道Uα和Uβ除了角度外還乘了一個PWM週期Ts(pHandle→PWMperiod)，結合代碼，wUAlpha多乘了2*sqrt(3)，wUBeta多乘了-2因此可以進一步簡化上述式子：

回憶一下程式碼中wX，wY與wZ三個變數和wUAlpha和wUBeta兩個變數的關係：

至此，可以計算UVW三相佔空比了，因為FOC庫定時器模式是中心對齊模式，所以計算佔空比時只計算一半就可以了：

FOC庫的變數格式是Q15格式，所以計算時要除以32768：

第6扇區計算佔空比的程式碼

wTimePhA = ( int32_t )( pHandle->PWMperiod ) / 4 + ( ( wY - wX ) / ( >int32_t )262144 ); 
wTimePhC = wTimePhA - wY / 131072; 
wTimePhB = wTimePhC + wX / 131072;

至此SVPWM演算法的原理與程式碼便可以連結起來了

圖7 六個基本空間向量合成的非失真條件

如圖7所示，外圓的大小為2*Udc/3,內圓的大小為Udc/sqrt(3)。根據圖5所示，狀態0和7合成的電壓向量為0，故TX=T=Ts/2當時，合成的電壓向量最大，此時合成的電壓向量邊界為圖7中的正六邊形。為了確保合成的電壓向量不會失真，合成的電壓向量不能超過圖7中的內圓，此時的電壓向量為Uref=2*Udc/3*sin(π/3)=Udc/sqrt(3)，這正是在之前推導過程中把sqrt(3)/Udc這個分量約掉的原因

SVPWM演算法分析到這就算完成了，這是FOC函式庫中比較難以理解的一部分，牽涉到的計算轉換比較多，把原理和程式碼對應起來屬實不容易，耗費了很久才整理出來這篇文章。知其然，也要知其所以然，只會用是遠遠不夠的，我們需要進一步挖掘其背後的原理，才能真正的靈活多變的解決產品問題，希望這篇文章能給喜歡研究原理的小夥伴帶來幫助

FOC5.4原始碼：https:// pan.baidu.com/s/1VIDh37

71 person(s) visited this page until now.

Back